数据结构与算法-归并排序

用户11147438

发布于 2025-05-29 12:45:24

7200

代码可运行

文章被收录于专栏：Linux系列Linux系列

运行总次数：0

代码可运行

💝💝💝首先，欢迎各位来到我的博客，很高兴能够在这里和您见面！希望您在这里不仅可以有所收获，同时也能感受到一份轻松欢乐的氛围，祝你生活愉快！

引言

归并排序（Merge Sort）是一种经典的排序算法，采用分治策略来实现高效排序。它将待排序的数组分成两个部分，递归地对这两个部分进行排序，然后再将排序后的两部分合并成一个有序数组。归并排序的时间复杂度为O(n log n)，并且是稳定的排序算法，这意味着相等的元素在排序前后相对顺序不变。本文将深入探讨归并排序的原理、实现步骤，并通过具体的案例代码详细说明归并排序的每一个细节。

一、归并排序的基本思想

归并排序的基本思想是：

分解：将数组分成尽可能小的子数组。
排序：对每个子数组进行排序。
合并：将排好序的子数组合并成更大的有序数组。

二、归并排序的步骤

假设有一个数组 arr 需要进行排序。

分解：如果数组长度大于1，则将其分成两个子数组。
递归排序：递归地对这两个子数组进行归并排序。
合并：将两个已排序的子数组合并成一个有序数组。

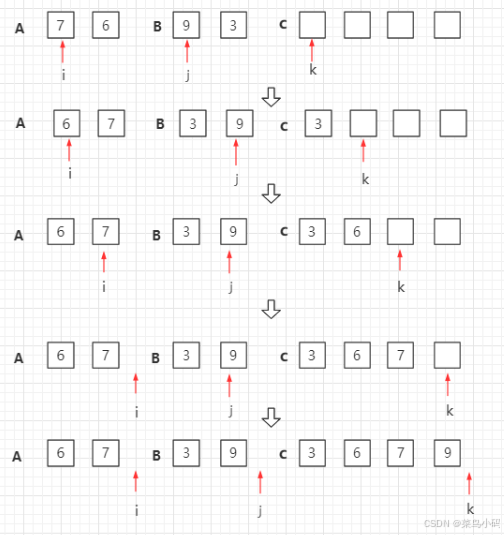
三、归并排序的实现

接下来，我们将通过一个示例来详细了解归并排序的实现步骤。

1. 示例数组

考虑一个整数数组 arr = [5, 2, 4, 6, 1, 3]。

2. 伪代码

以下是归并排序的基本伪代码：

function merge_sort(arr):
    if length(arr) <= 1:
        return arr
    else:
        mid = length(arr) // 2
        left = merge_sort(arr[0:mid])
        right = merge_sort(arr[mid:])
        return merge(left, right)

function merge(left, right):
    result = []
    i = j = 0
    while i < length(left) and j < length(right):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    result.extend(left[i:])
    result.extend(right[j:])
    return result

3. Python 实现

下面是一个使用Python编写的归并排序算法的具体实现：

def merge_sort(arr):
    # 如果数组只有一个元素或为空，直接返回
    if len(arr) <= 1:
        return arr
    
    # 分解数组
    mid = len(arr) // 2
    left = arr[:mid]
    right = arr[mid:]
    
    # 递归排序左右两部分
    left_sorted = merge_sort(left)
    right_sorted = merge_sort(right)
    
    # 合并两个有序数组
    return merge(left_sorted, right_sorted)

def merge(left, right):
    result = []
    i = j = 0
    
    # 合并两个数组
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1
    
    # 添加剩余的元素
    result.extend(left[i:])
    result.extend(right[j:])
    
    return result

# 示例数组
arr = [5, 2, 4, 6, 1, 3]
# 调用函数
sorted_arr = merge_sort(arr)
print(sorted_arr)